3.2 Variabili aleatorie normali (o gaussiane)

Scegliendo Normal nel box Distribution visualizziamo la schermata per il calcolo di probabilità relative a una variabile aleatoria normale (vedi Figura 3.4), la quale di fatto rappresenta una versione elettronica e più generale della tavola della normale standard presentata nel corso.

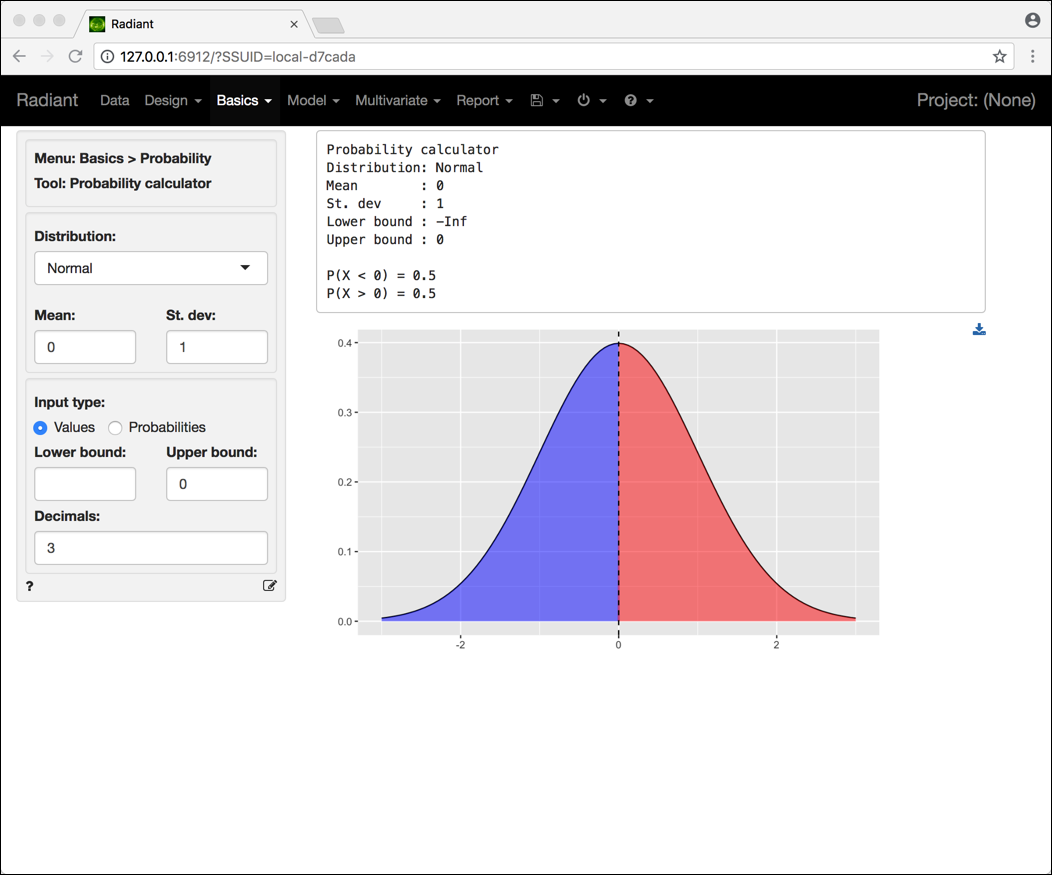
Figura 3.4: Schermata Radiant per il calcolo di probabilità relative a una variabile aleatoria normale.

Nel caso ci interessi calcolare una probabilità relativa ad un intervallo di valori, dobbiamo cliccare su Input type $\rightarrow$ Values, mentre se ci interessasse la situazione opposta, ovvero il calcolo degli estremi dell’intervallo corrispondente ad un certo valore di probabilità, dobbiamo scegliere Input type $\rightarrow$ Probabilities. Vediamo un esempio per ciascuno di questi casi.

Supponiamo di voler calcolare la probabilità che una variabile aleatoria \(X\) distribuita secondo una normale con media 50 e varianza 64, ovvero \(X \sim N(\mu = 50, \sigma^2 = 64)\), assuma valori nell’intervallo \((45, 60)\). In questo caso dobbiamo:

• inserire i valori dei parametri nei box Mean e St. dev.³⁴
• se non è già selezionato, cliccare su Input type $\rightarrow$ Values
• nei box Lower bound e Upper bound inserire rispettivamente 45 e 60
• suggeriamo anche di aumentare a 4 il numero di cifre decimali mostrate (Decimals)

La schermata che ne risulta è riportata in Figura 3.5.

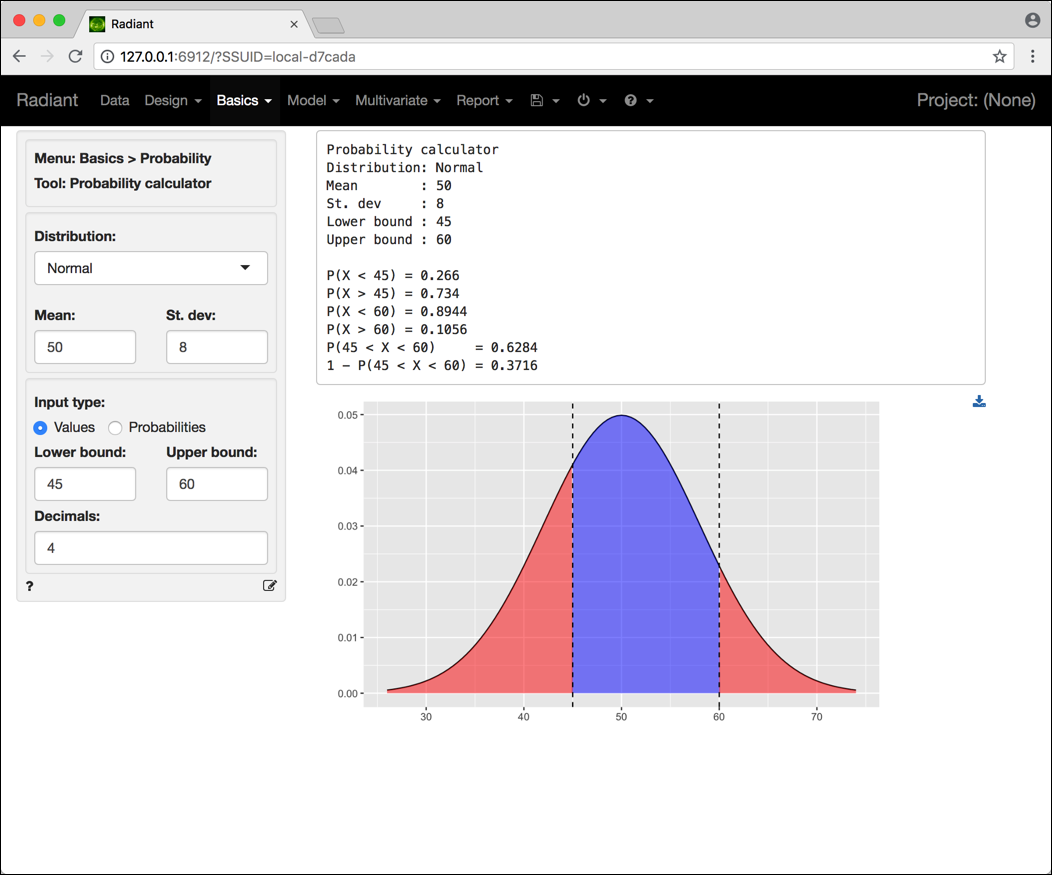
Figura 3.5: Schermata Radiant per il calcolo di probabilità relative a una variabile aleatoria normale.

Il risultato cercato è riportato come P(45 < X < 60) = 0.6284.

Vi facciamo notare che se lasciate vuoto uno dei box Lower bound o Upper bound, ciò viene interpretato da Radiant come un intervallo illimitato a sinistra o a destra³⁵.

Se invece volessimo ricavare la probabilità corrispondente ad un dato intervallo di valori, dobbiamo selezionare Input type $\rightarrow$ Probabilities. Ad esempio, continuando con l’esempio precedente, supponiamo ci interessi ottenere il valore \(x\) della variabile aleatoria \(X\) che non sarà superato con probabilità pari a 95%, ovvero il valore \(x\) tale che \(P(X \le x) = 0.95\). In questo caso dobbiamo:

• controllare che i valori dei parametri nei box Mean e St. dev. siano quelli corretti
• se non è già selezionato, cliccare su Input type $\rightarrow$ Probabilities
• nel box Upper bound inserire il valore 0.95 e indifferentemente lasciare vuoto o inserire il valore 0 nel box Lower bound
• verificare di aver indicato 4 cifre decimali nel box Decimals

La schermata che ne risulta è riportata in Figura 3.6.

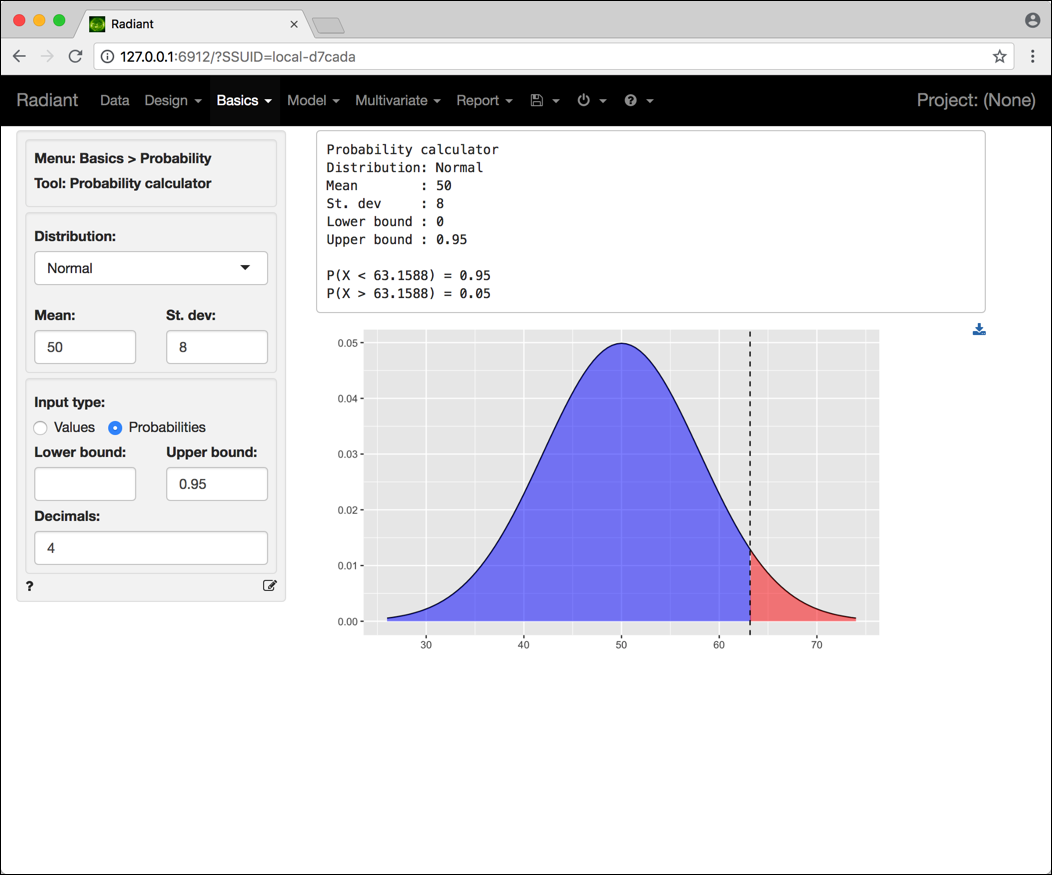
Figura 3.6: Schermata Radiant per il calcolo di probabilità relative a una variabile aleatoria normale.

Il risultato cercato è riportato come P(X < 63.1588) = 0.95, ovvero \(x = 63.1588\).

---

34. Attenzione, Radiant richiede di inserire il valore della deviazione standard e non della varianza. Nel nostro caso \(\sigma = \sqrt{64} = 8\).↩

35. In R, e quindi anche in Radiant, un valore infinito viene indicato come Inf.↩