3.1 Variabili aleatorie binomiali

Per effettuare calcoli probabilistici con una variabile aleatoria binomiale, selezionate nel box Distribution la voce Binomial. La schermata che vi si presenterà è riportata in Figura 3.2.

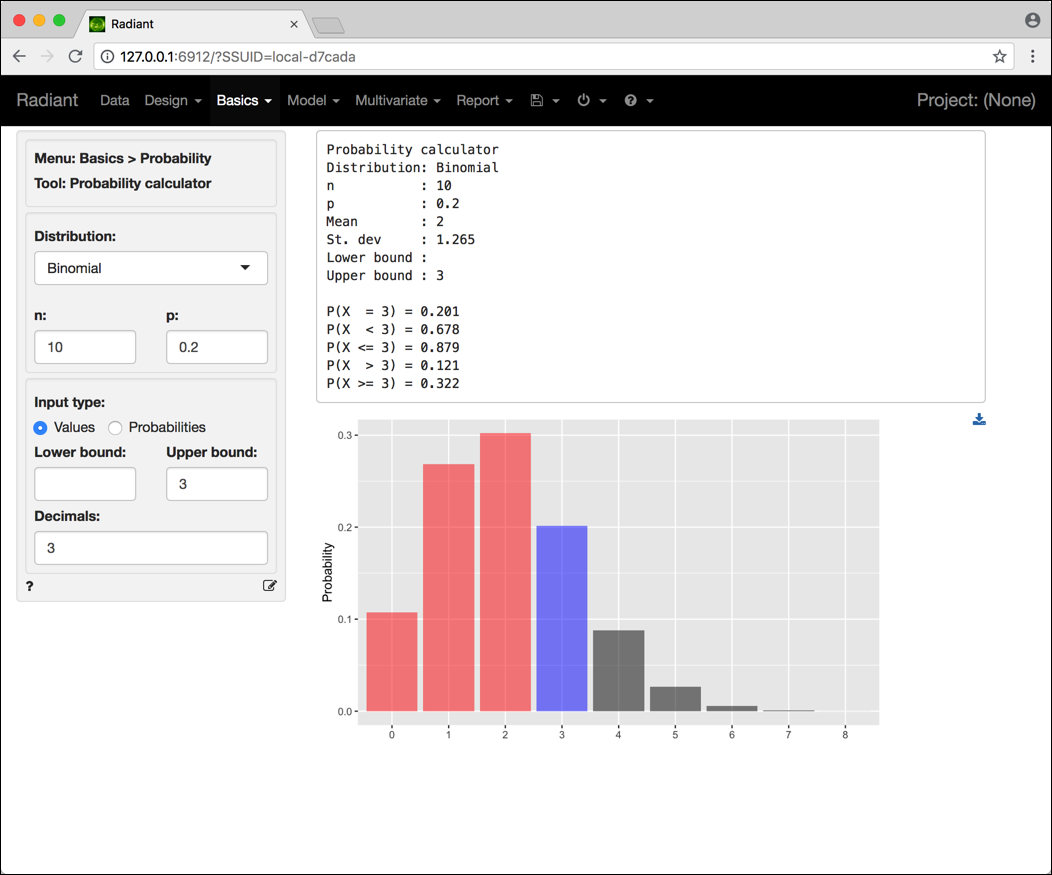
Figura 3.2: Schermata Radiant per il calcolo di probabilità relative a una variabile aleatoria binomiale.

La schermata riporta i valori dei parametri della distribuzione, ovvero il numero di prove bernoulliane n e la probabilità di successo p in ognuna delle prove, e il corrispondente grafico della funzione di probabilità con le barre colorate in funzione dei valori riportati nei box Lower bound e Upper bound. Nella parte centrale della schermata sono riportati i valori della media e delle deviazione standard e le probabilità relative ad alcuni intervalli determinati sempre tramite i box Lower bound e Upper bound.

Supponiamo di voler calcolare la probabilità con cui una variabile aleatoria binomiale di parametri \(n = 8\) e \(p = 0.3\) assuma un valore compreso nell’intervallo \([4, 7)\) (l’intervallo è aperto solo a destra). In questo caso dobbiamo:

• inserire i valori dei parametri nei box n e p
• se non è già selezionato, cliccare su Input type $\rightarrow$ Values
• nei box Lower bound e Upper bound inserire rispettivamente 4 e 7
• suggeriamo anche di aumentare a 4 il numero di cifre decimali mostrate (Decimals)

La schermata che ne risulta è riportata in Figura 3.3.

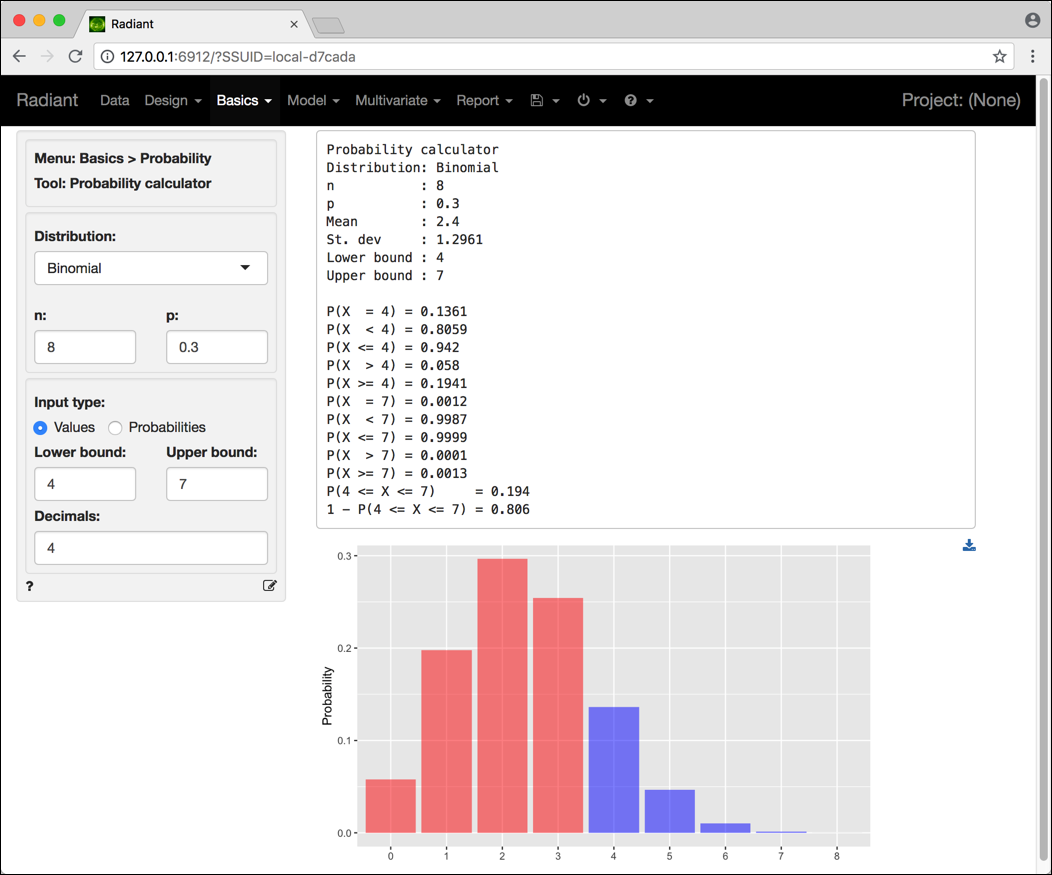
Figura 3.3: Schermata Radiant per il calcolo di probabilità relative a una variabile aleatoria binomiale.

La probabilità che ci interessa, ovvero \(P(4 \le X < 7)\) in cui il valore 7 è escluso, non è riportata nella tabella, la quale riporta invece \(P(4 \le X \le 7)\), in cui invece il valore 7 è incluso. La questione è facilmente risolta, perché la stessa tabella indica anche quanto vale \(P(X = 7)\), che quindi basta sottrarre da \(P(4 \le X \le 7)\) per ottenere il risultato cercato, ovvero

\[\begin{equation*} P(4 \le X < 7) = P(4 \le X \le 7) - P(X = 7) = 0.1940 - 0.0012 = 0.1928. \end{equation*}\]

In modo equivalente, è possibile ottenere lo stesso risultato inserendo direttamente i valori 4 e 6 nei box Lower bound e Upper bound.

Rimane inteso che questa stessa schermata può essere utilizzata anche per variabili aleatorie bernoulliane semplicemente fissando ad 1 il numero di prove n.