4.5 Test sulla bontà di adattamento (probabilità completamente specificate)

Il test sulla bontà di adattamento consente di valutare se una distribuzione di probabilità osservata per una variabile aleatoria discreta (con supporto finito) possa essere considerata “compatibile” con una distribuzione di probabilità teorica definita a priori. Radiant consente di effettuare tale test con il comando Basics \(\rightarrow\) Goodness of fit. Nella schermata che appare, è necessario inserire le seguenti informazioni:

• la variabile nel data set che contiene i dati con cui effettuare l’analisi (box Select a categorical variable)
• le probabilità che definiscono la distribuzione teorica con cui confrontare quella osservata (box Probabilities); queste probabilità devono essere inserite come numeri compresi tra 0 e 1, la cui somma deve essere pari a 1 e il cui numero deve essere pari alle categorie osservate per la variabile indicata nel box precedente
• il tipo di output da mostrare (box Observed per le frequenze osservate, Expected per quelle attese sotto l’ipotesi nulla, Chi-squared per il contributo al calcolo dell’indice \(\chi^2\) di ogni categoria³⁸)

Consideriamo ancora una volta il data frame forbes94 e in particolare la variabile MasterPhd. Proviamo a testare l’ipotesi nulla che nella popolazione da cui questi CEO provengono la quota percentuale di essi con e senza un Master o un PhD sia la stessa, ovvero 50% e 50%. La Figura 4.6 mostra le selezioni da effettuare e l’output corrispondente.

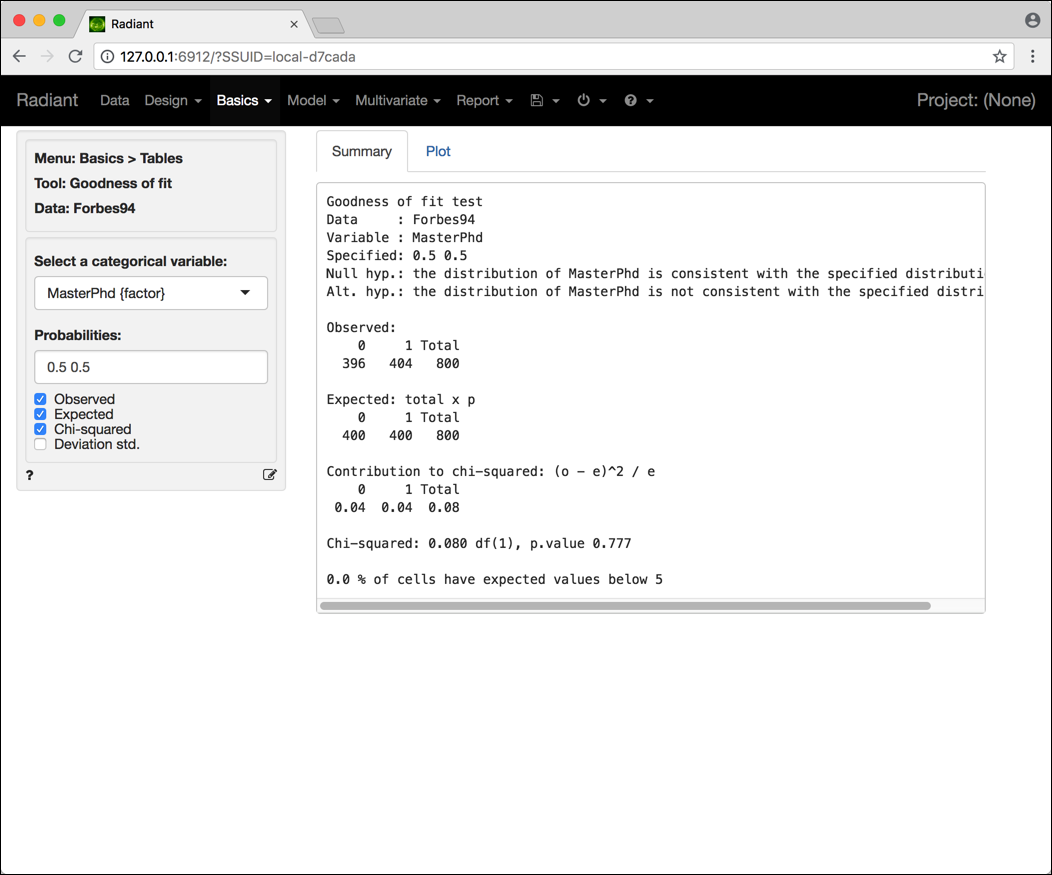
Figura 4.6: Schermata Radiant per il test sulla bontà di adattamento.

L’output riporta un p-value pari a 0.777, ovvero i dati non consentono di scartare l’ipotesi nulla e quindi non si hanno sufficienti prove a sfavore dell’affermazione che la quota percentuale di CEO con un Master o un PhD sia diversa dal 50%³⁹.

Vediamo ora un secondo esempio: il file market_share.RData contiene l’omonimo data frame, il quale include un’unica variabile chiamata Brand. Questa colonna raccoglie il brand di un certo prodotto acquistato da 400 clienti di un grossista. Tali dati sono relativi a clienti posti in una nuova zona di vendita. Il grossista vuole valutare se la politica di magazzino dei 4 brand che ha utilizzato nella sua zona storica di vendita possa essere replicata anche nella nuova zona. Per fare ciò, il grossista desidera confrontare la distribuzione osservata per il campione di 400 clienti dalla nuova zona con le preferenze dei clienti della zona storica, ovvero 20% per il brand A, 35% per il brand B, 30% per il brand C e 15% per il brand D. La distribuzione di frequenze dei brand acquistati dai clienti inclusi nel campione è riportata in Figura 4.7.

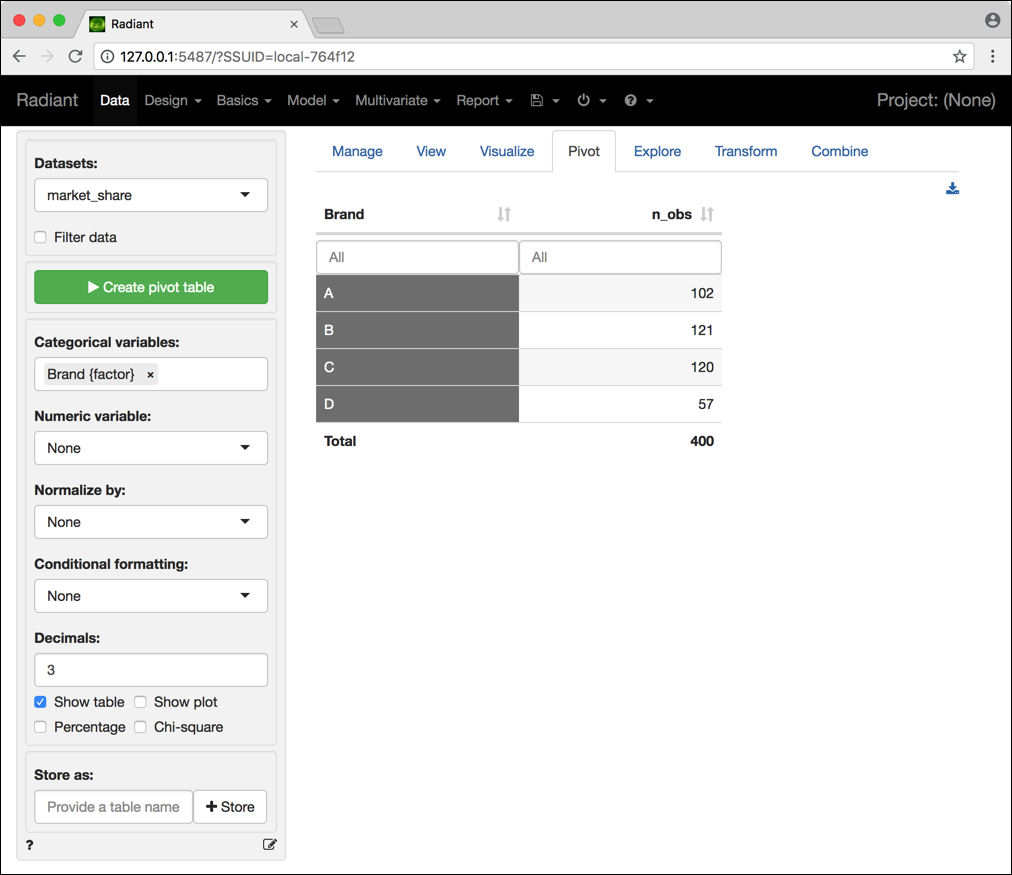
Figura 4.7: Distribuzione di frequenze dei brand acquistati dai clienti inclusi nel data frame market_share.

Dopo aver selezionato la variabile Brand nel box Select a categorical variable e inserito i valori .2 .35 .3 .15 nel box Probabilities, è possibile visualizzare vari risultati relativi al test sulla bontà di adattamento (si veda Figura 4.8).

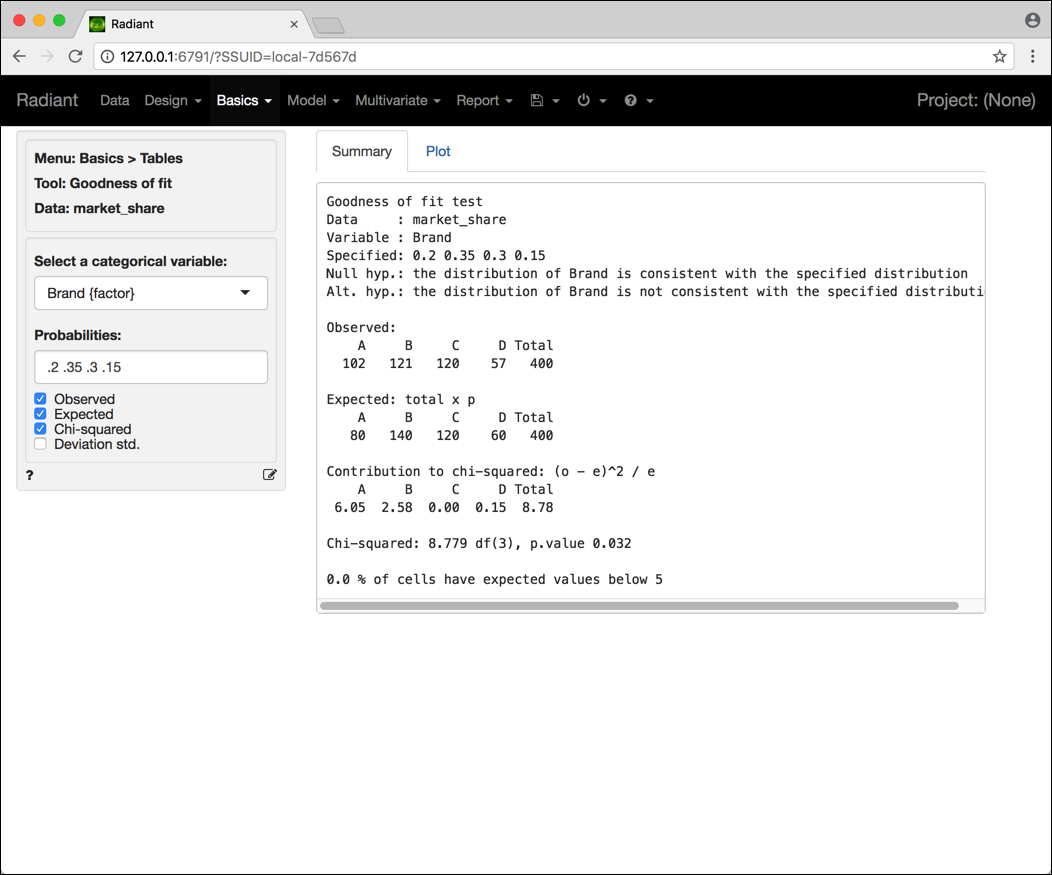
Figura 4.8: Schermata Radiant per il test sulla bontà di adattamento.

Adottando un livello di significatività del 5% possiamo concludere che i dati (p-value = \(0.032 < 0.05\)) supportano la conclusione che la distribuzione delle preferenze nella nuova zona non sia compatibile con quelle della zona storica e che quindi non sia possibile replicare la stessa politica di magazzino.

Concludiamo questa sezione facendovi notare che Radiant riporta sempre nell’output di questo test una valutazione delle ipotesi su cui è basato il test. Per l’esempio precedente, infatti, riporta che

0.0 \% of cells have expected values below 5,

quindi l’approssimazione sulla base della quale il p-value è calcolato si può ritenere accettabile.

---

38. La schermata consente anche di visualizzare altri risultati, indicati come Deviation std., che non sono stati illustrati nel corso e che quindi non discuteremo neppure in questa sede.↩

39. Notate che il p-value ottenuto è di fatto uguale a quello che otterremo con un test su una singola proporzione, perché in questo caso la variabile che stiamo considerando assume solo due categorie.↩