4.1 Inferenza sulla media di una popolazione normale

E’ possibile fare inferenza su una media \(\mu\) di una popolazione normale assumendo che la varianza \(\sigma^2\) della popolazione sia nota oppure no. In questa sezione ci occupiamo solo del secondo caso perché si tratta della situazione più frequente e rilevante nella pratica dell’analisi dei dati. Inoltre, né R né Radiant mettono a disposizione comandi che consentono di ottenere rapidamente i risultati nel caso in cui la varianza fosse nota.

Per il caso di una singola media per una popolazione normale, Radiant include il menu Basics \(\rightarrow\) Single mean. Vediamo subito un esempio usando ancora una volta i dati contenuti nel data frame forbes94. In particolare, definiamo una nuova variabile che chiamiamo ROS, ovvero return on sales, calcolata come il rapporto percentuale dei profitti rispetto ai ricavi di vendita, che esprime la redditività aziendale in relazione alla capacità remunerativa del flusso dei ricavi. Per creare la nuova variabile ROS in Radiant dovete selezionare il tab Transform del menu Data, quindi selezionare la voce Create nel box Transformation type, definire la nuova variabile digitando ROS = Profits/Sales*100 nel box Create, premere INVIO ed infine cliccare sul pulsante verde +Store per aggiungere la variabile al data frame.

La schermata per l’inferenza sulla media di una popolazione normale, di cui mostriamo in Figura 4.1 un esempio per la variabile ROS, richiede di:

• selezionare la variabile da analizzare nel box Variable (select one)
• scegliere il tipo di ipotesi alternativa da testare nel box Alternative hypothesis; i valori possibili sono Two sided, Less than e Greater than
• scegliere il livello di confidenza con lo slider Confidence level
• infine, indicare il valore da testare sotto l’ipotesi nulla nel box Comparison value

Radiant calcola automaticamente sia l’intervallo di confidenza sia il test sulla media. Nell’esempio relativo a ROS il test che eseguiamo è

\[\begin{equation*} H_0: \mu = 0 \qquad \mbox{vs.} \qquad H_1: \mu \ne 0, \end{equation*}\]

dove \(\mu\) indica la media non nota della variabile ROS nella popolazione.

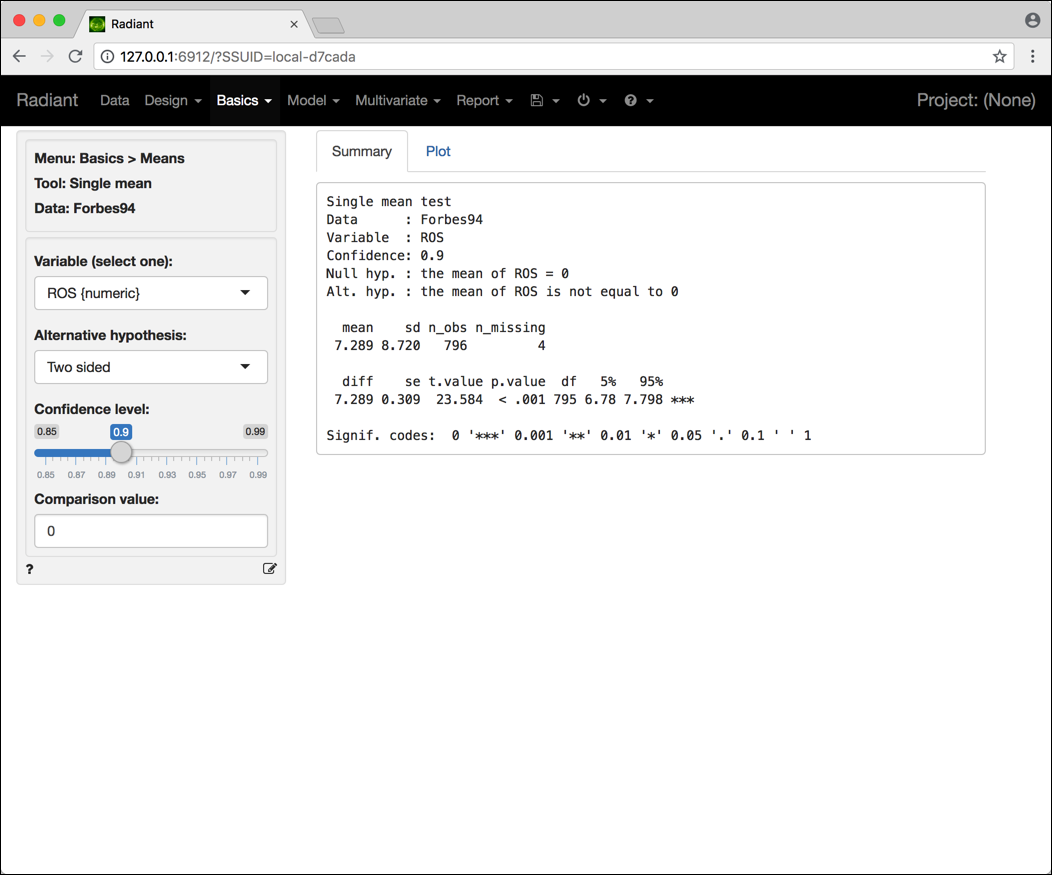
Figura 4.1: Schermata Radiant per l’inferenza sulla media di una popolazione normale.

I risultati indicano che l’intervallo di confidenza al 90% per \(\mu\) è pari a \((6.7799, 7.7978)\), mentre il test restituisce un p-value molto piccolo, riportato come < 0.001, il quale permette di rifiutare ampiamente l’ipotesi nulla anche decidendo di usare un livello di significatività \(\alpha\) di 0.01.

Nel caso si scegliesse un test unilaterale, l’intervallo di confidenza restituito da Radiant non è quello standard (ovvero bilaterale) illustrato nel corso e quindi non sarà qui commentato.