4.3 Inferenza sul confronto tra le medie di due popolazioni normali

Il caso della differenza tra due medie è uno di quelli più utilizzati nelle applicazioni e nel corso ne sono state presentate alcune varianti, in particolare:

• confronto tra le medie di due popolazioni normali con varianze note, campioni indipendenti
• confronto tra le medie di due popolazioni normali con varianze non note ma assunte uguali, campioni indipendenti
• confronto tra le medie di due popolazioni normali con varianze non note, campioni dipendenti

In Radiant non sono disponibili strumenti per il primo caso, che quindi non presenteremo qui, mentre per il secondo offre solo la possibilità di confrontare due medie nel caso in cui le varianze siano non note e diverse. Questa situazione non è stata presentata nel corso perché i calcoli richiesti sono impegnativi, ma dal momento che ora sarà Radiant a fare i conti, ne discuteremo comunque l’applicazione.

4.3.1 Campioni indipendenti

Per confrontare le medie di due popolazioni normali con varianze non note in Radiant possiamo utilizzare il menu Basics \(\rightarrow\) Compare means, ma rispetto al caso di una singola media dovremo ora fornire i seguenti input:

• nel box Select a factor or numeric variable dobbiamo indicare la variabile (tipicamente di tipo factor) che identifica i gruppi di cui vogliamo confrontare le medie
• nel successivo box Numeric variable dobbiamo selezionare la variabile numerica di cui vogliamo confrontare le medie
• nel box Alternative hypothesis indichiamo il tipo di ipotesi alternativa che vogliamo testare; i valori possibili sono Two sided per il test bilaterale e Less than o Greater than per i test unilaterali
• lo slider Confidence level ci permette di scegliere il livello di confidenza
• il checkbox Show additional statistics permette di visualizzare altri risultati (ad esempio gli intervalli di confidenza, che quindi non sono proposti in automatico)
• dobbiamo verificare che sia selezionato il pulsante independent nella sezione Sample type
• dobbiamo infine verificare che sia selezionato il pulsante t-test nella sezione Test type

Vediamo subito un esempio in cui confrontiamo la media della variabile ROS nei due gruppi identificati dalla variabile MasterPhd, che indica i CEO che nel 1994 possedevano un titolo di Master o di PhD. Calcoliamo l’intervallo di confidenza al 95% e effettuiamo il test per verificare se le medie delle rispettive popolazioni siano uguali, ovvero

\[\begin{equation*} H_0: \mu_{(\mbox{MasterPhd}=0)} = \mu_{(\mbox{MasterPhd}=1)} \quad \mbox{vs.} \quad H_1: \mu_{(\mbox{MasterPhd}=0)} \ne \mu_{(\mbox{MasterPhd}=1)}. \end{equation*}\]

I risultati sono riportati in Figura 4.3.

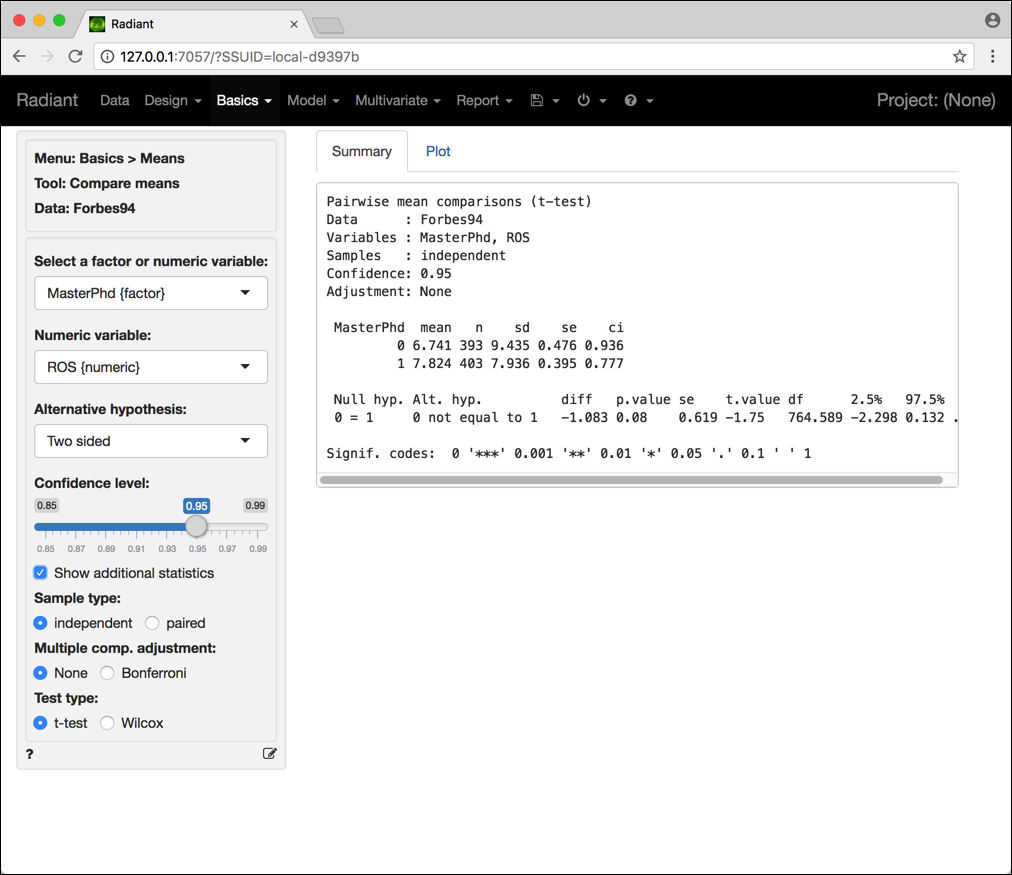
Figura 4.3: Schermata Radiant per il test sul confronto tra due medie (campioni indipendenti).

La media campionaria nel secondo campione (MasterPhd = 1) risulta essere maggiore che nel primo (MasterPhd = 0) e i risultati del test suggeriscono che sembrano esserci differenze significative tra le medie del ROS nelle due popolazioni di aziende, quelle il cui CEO non ha un Master o un Phd e quelle in cui il CEO ha un Master o un Phd, ma solo se decidiamo di usare un livello di significatività del 10% (il p-value del test risulta infatti pari a 0.08³⁷).

Il tab Plot dello stesso menu consente di visualizzare i risultati in forma grafica attravero diversi tipi di grafici (Scatter, Box, Density, Bar). La Figura 4.4 mostra alcuni di questi grafici per l’esempio precedente.

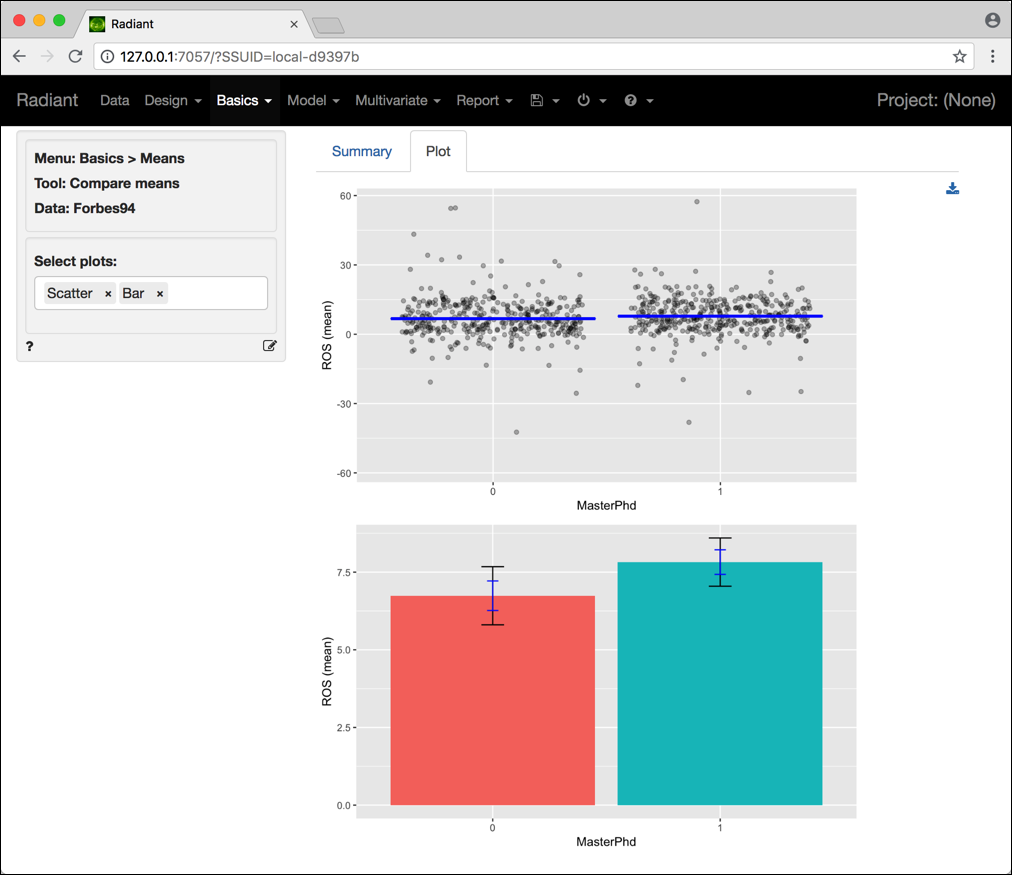
Figura 4.4: Schermata Radiant per il test sul confronto tra due medie (campioni indipendenti).

4.3.2 Campioni dipendenti

Un’ulteriore situazione che si può incontrare in pratica è quella in cui le medie da confrontare riguardano la stessa popolazione che però è stata osservata in due momenti o, più in generale, sotto due condizioni diverse. Questo è il caso di campioni dipendenti, poiché in tale contesto il medesimo campione viene osservato due volte. Nello stesso ambito è compreso anche il caso in cui i due campioni, pur essendo diversi, sono stati “appaiati” in modo da approssimare il più precisamente possibile la situazione di un singolo campione osservato ripetutamente. In entrambi i contesti (stesso campione osservato due volte o due campioni appaiati), i campioni devono contenere lo stesso numero di osservazioni.

Anche questo caso può essere gestito in Radiant attraverso il comando Basics \(\rightarrow\) Compare means descritto nella sezione precedente, salvo che ora dovremo selezionare il checkbox denominato paired.

Vediamo un esempio usando i dati contenuti nel data frame supermarket nell’omonimo file. Il data frame contiene il numero di clienti che hanno visitato un campione di 10 negozi di una catena di supermercati in due giorni diversi, in uno solo dei quali era attiva una promozione. In particolare, il data frame contiene le seguenti variabili:

• store, che indica il negozio a cui l’osservazione si riferisce
• customers, che indica il numero di clienti che hanno visitato ognuno dei negozi nei due giorni
• program, che indica invece il giorno in cui la promozione era attiva

L’obiettivo di questo esempio è valutare se la promozione sia stata efficace in termini di aumento del numero medio di clienti che hanno visitato i negozi. Calcoleremo sia l’intervallo di confidenza al 90% sia il seguente test

\[\begin{equation*} H_0: \mu_X - \mu_Y \ge 0 \qquad \mbox{vs.} \qquad H_1: \mu_X - \mu_Y < 0, \end{equation*}\]

dove \(X\) indica la popolazione di negozi in cui la promozione non è attiva, mentre \(Y\) denota la popolazione di negozi in cui la promozione è attiva.

Dopo aver caricato i dati e scelto il comando Basics \(\rightarrow\) Compare means:

• nel box Select a factor or numeric variable scegliamo program come variabile che identifica i due campioni
• nel successivo box Numeric variable selezionamo la variabile numerica customers
• nel box Alternative hypothesis indichiamo il tipo di ipotesi alternativa che vogliamo testare; in particolare in questo esempio scegliamo Less than perché ci interessa verificare se i dati suggeriscono che la promozione ha permesso di aumentare il numero medio di visite ai negozi
• lo slider Confidence level ci permette di indicare il livello di confidenza che ci interessa usare
• il checkbox Show additional statistics permette di visualizzare ulteriori risultati
• dobbiamo verificare che sia selezionato il pulsante paired nella sezione Sample type
• dobbiamo infine verificare che sia selezionato il pulsante t-test nella sezione Test type

La Figura 4.5 mostra i risultati dell’analisi:

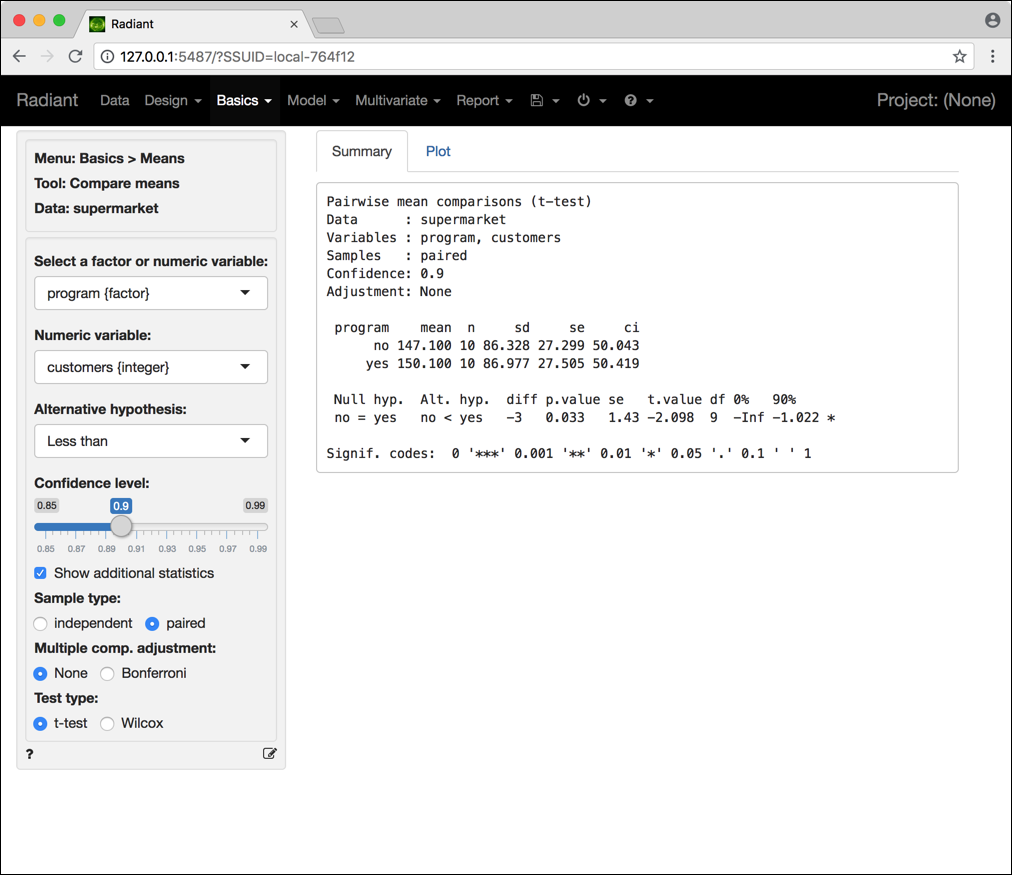
Figura 4.5: Schermata Radiant per il test sul confronto tra due medie (campioni dipendenti).

I risultati indicano che, assumendo di usare un livello di significatività del 5%, la promozione sembra avere avuto un effetto significativo sulla media del numero di visite poiché il p-value del test (0.033) è inferiore a 0.05.

Concludiamo questa sezione evidenziando che in questi risultati l’intervallo di confidenza che viene restituito da Radiant è quello unilaterale, che non consideriamo in questo manuale.

---

37. Ricordiamo che Radiant include solo il caso di varianza non note e diverse.↩